Triángulo de monedas

Con 10 monedas hemos construido un triángulo equilátero como el de la figura. Desplazando sólo tres monedas de lugar, se debe conseguir otro triángulo equilátero pero invertido.

¿Sabes hacerlo?

  

Cube It

Este juego consiste en pasar el cubo verde por encima de todos los cubos rojos (para desplazarlo hacer clic con el ratón en el cubo adyacente). Pero cuidado con los cubos rojos, se caerán en cuanto paséis por ellos.

Torres de Hanoi

Las Torres de Hanói es un juego de lógica que inventó el matemático francés Éduard Lucas en 1883.

El juego consta de tres varillas verticales, en una de las cuales se apila un número de discos de mayor a menor diámetro, quedando las otras dos varillas libres. El juego consiste en pasar todos los discos de la varilla ocupada a una de las otras varillas libres. Las reglas son las siguientes.

- Sólo se puede mover un disco cada vez.
- Los discos sólo se pueden colocar sobre otros de mayor diámetro o en una varilla libre.
- Sólo se pueden desplazar los discos que se encuentran en la parte superior de las varillas.

El número mínimo de movimientos para resolver el juego es:

- Con 2 discos →   3 movimientos.
- Con 3 discos →   7 movimientos.
- Con 4 discos → 15 movimientos.
- ...

El número de movimientos (o sea, la complejidad del juego) crece exponencialmente con el número de discos, por lo que debéis empezar con pocos e ir poco a poco aumentando la dificultad.

Para jugar online haz clic en la imagen (www.uterra.com).

The equator

Un juego matemático en el que tendréis que sumar, restar, multiplicar y dividir a gran velocidad para poder eliminar el mayor número posible de piezas y conseguir pasar de nivel. Consiste en seleccionar tres números adyacentes de forma que el tercero sea el resultado de operar los dos primeros.

Haz clic en la imagen para comenzar a jugar.

El número 142857

Si multiplicamos el número 142857 por 7 nos da 999999.
Pensaréis que esto no tiene nada del otro mundo, pero vamos a multiplicar este número por 2, 3, 4, 5 y 6.

1 * 142857 = 142857
2 * 142857 = 285714
3 * 142857 = 428571
4 * 142857 = 571428
5 * 142857 = 714285
6 * 142857 = 857142

Al observar los resultados nos percatamos de que contienen los mismos dígitos en el mismo orden.

Pero sigamos con este número, si comparáis los resultados de las siguientes divisiones con los obtenidos en las multiplicaciones os sorprenderéis.

1/7 = 0.142857 142857 142857 … (1 * 142857 = 142857)
2/7 = 0.285714 285714 285714 … (2 * 142857 = 285714)
3/7 = 0.428571 428571 428571 … (3 * 142857 = 428571)
4/7 = 0.571428 571428 571428 … (4 * 142857 = 571428)
5/7 = 0.714285 714285 714285 … (5 * 142857 = 714285)
6/7 = 0.857142 857142 857142 … (6 * 142857 = 857142)

Sí, todos los resultados obtenidos son números periódicos, y además su periodo coincide con el resultado de la multiplicación.

Pero aún hay más: 142+857=999

La tabla de multiplicar del 9.

¿Cuántas veces habréis estudiado de memoria la tabla del 9?, y seguro que, como estaba de las últimas, es una de las que más trabajo os costó aprender.

Fijaos en este vídeo y veréis como no era tan difícil.

Si observáis los resultados de las multiplicaciones os percataréis de algo más. ¿Sabríais decirnos de qué se trata?

Cuadrados de números terminados en 5

Esta es una actividad que te resultará muy útil en cálculo mental. Se trata de encontrar el cuadrado de un número de dos cifras que termine en 5.

Vamos a verlo con un ejemplo.
¿Cuánto es 15 al cuadrado? Multiplicando 15 x 15 obtenemos que es 225.
Pero ahora viene lo interesante, ¿puedo obtener este resultado mediante una regla, sin necesidad de realizar la multiplicación?

Vamos a multiplicar el número de decenas, en este caso uno, por el siguiente número, o sea, dos.
1x2=2

A continuación añadimos el número 25. Como podéis ver se obtiene el número buscado, en este caso es 225.

Os animamos a que apliquéis este método para calcular otros cuadrados de números de dos cifras que terminen en 5.

¡Poned vuestros comentarios con los ejemplos que realicéis!

Sudoku

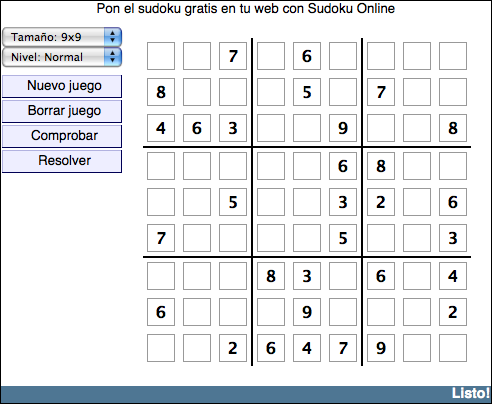
Sudoku es un pasatiempo que se popularizó en Japón en 1986, y se dio a conocer internacionalmente en 2005. El objetivo del Sudoku es rellenar las casillas vacías de una cuadrícula de 9 × 9 celdas (81 casillas) dividida en subcuadrículas de 3 × 3 (también llamadas "cajas" o "regiones") con las cifras del 1 al 9.

Las reglas son las siguientes:

• Hay que completar cada casilla vacía con un solo número del 1 al 9. 
• En una misma fila no puede haber números repetidos. 
• En una misma columna no puede haber números repetidos. 
• En una misma región no puede haber números repetidos. 
• La solución de un Sudoku es única. 

De alguna forma el Sudoku se basa en la búsqueda de la combinación numérica perfecta. Hay diferentes niveles de dificultad y la resolución del problema requiere paciencia y ciertas dotes lógicas. Profesores de todo el mundo lo recomiendan como método para desarrollar el razonamiento lógico.

En realidad, no es obligatorio usar números, sino que también pueden utilizarse letras, formas o colores sin alterar las reglas, pero se utilizan números por conveniencia. Aunque la cuadrícula más común sea la de 9×9 con regiones de 3×3, también se utilizan otros tamaños.

Aquí tenéis el juego para que practiquéis online.

La Lógica Simbólica de Lewis Carroll

Hace 145 años que se publicó por primera vez  "Las aventuras de Alicia en el país de las maravillas" (Alice’s Adventures in Wonderland), a menudo abreviado como “Alicia en el País de las Maravillas”. El 26 de noviembre de 1865, Charles Lutwidge Dodgson publicó bajo al pseudónimo de Lewis Carroll, esta célebre obra, considerada por muchos como uno de los cuentos infantiles más populares del mundo. Alicia ha fascinado tanto a lectores jóvenes como adultos de generación en generación, y su lectura se ha convertido en una deliciosa obligación. Prácticamente no hay biblioteca o librería en el mundo donde no se pueda conseguir.

Pocos años despues de la aparición de "Alicia en el país de las maravillas, LEWIS CARROL publicaría, como segunda parte, "A través del espejo y lo que Alicia encontró al otro lado", superior a la primera en la utilización de la técnica narrativa y el dominio de las formas expresivas. Cuento pensado para los niños pero leído --y citado hasta el cansancio-- por los adultos.

Lewis Carroll fue una persona singular, lógico y matemático (profesor de la universidad de Oxford), novelista, soñador de países maravillosos, de mundos de espejo, así como un apasionado de la fotografía. Como matemático escribió muchos libros: Compendio de Geometría Algebraica Plana, Tratado elemental de determinantes, etc.. Pero lo que más le apasionó fue la lógica. Durante las dos ultimas décadas del siglo XIX, Lewis Carroll escribió una obra de lógica muy interesante, titulada Lógica Simbólica (Symbolic Logic), la Primera Parte fue publicada en 1896 (Symbolic Logic by Lewis Carroll. Part I, Elementary), y la Segunda Parte, en la cual estuvo trabajando hasta el día de su muerte, en 1977 (Part II, Advanced, never previously published. Edited by W. W. Bartley. Clarkson N. Potter, Inc. Publishers, New York).

La Lógica Simbólica de Carroll es una obra de transición entre la lógica tradicional y la lógica moderna. La lógica de Carroll no es una lógica que se preocupe por los fundamentos de las Matemáticas, sino mas bien una ayuda instruccional de utilidad pedagógica. Una lógica para detectives. Carroll consideraba la Lógica como una de las más altas recreaciones de la mente, por encima de los juegos y los rompecabezas. Podríamos casi hablar de una Lógica Lúdica. La Lógica Simbólica es un libro lúdico, un libro que se va ejecutando a sí mismo según vamos resolviendo sus problemas y acertijos.

A continuación os vamos a poner algunos de estos juegos de lógica publicados en el libro de Lewis Carroll "LÓGICA SIMBÓLICA".

¿ C u á l .. e s .. l a .. c o n c l u s i ó n .. c o r r e c t a ?

En cada actividad encontrarás dos frases y después dos posibles conclusiones. Tú debes decidir cuál es la correcta, es decir cuál es la que se deduce lógicamente de las frases anteriores. Es muy importante señalar que no importa si las frases o las conclusiones son verdaderas o falsas, se trata únicamente de averiguar cuál conclusión es la que se obtiene de las dos premisas dadas.

1 Todos los leones son feroces
2 Algunos leones no beben  café
¿Cuál es la conclusión correcta?
a Algunas criaturas que beben café no son feroces
b Algunas criaturas feroces no beben café


1 Algunos sueños son terribles

2 Ningún  borrego es terrible

¿Cuál es la conclusión correcta?
a Algunos sueños no son borregos
b Algunos borregos no son sueños

J u g a n d o .. c o n .. p a l a b r a s

El objetivo del juego es transformar una palabra en otra siguiendo estas reglas:

1 En cada paso únicamente se puede cambiar una letra.
2 Todas las palabras deberán tener significado.
3 No se admiten faltas de ortografía.
4 No se admiten nombres propios.
5 No se puede agregar ni quitar letras

Ejemplos:

Transformar la palabra  SOL en la palabra  MAR

SOL
SAL se cambió la O por una A
MAL se cambió la S por una M
MAR se cambió la L por una R

En esta cadena, se cambió una letra en cada paso, todas las palabras tienen significado, no hay faltas de ortografía, no agregamos ni quitamos letras y no usamos nombres propios. Es decir seguimos todas las reglas.

Transformar la palabra  LUNA en la palabra  FOCO

LUNA
LONA se cambió la U por la O
LOCA se cambió la N por la C
FOCA se cambió la L por la F
FOCO se cambió la A por la O

Es muy importante darse cuenta de que hay muchos caminos para llegar de una palabra a otra. Unos son largos, otros cortos, unos difíciles y otros fáciles, pero todos son correctos si cumplen las reglas.
¡A jugar!

1 Transformar la palabra CALOR en la palabra VOLAR
2 Transformar la palabra AMAR en la palabra USAR
3 Transformar la palabra  en la palabra CUNA
4 Transformar la palabra  PLATO en la palabra PLANO
5 Transformar la palabra CASA en la palabra POZO
6 Transformar la palabra CURA en la palabra RUSO

Podéis pensar vuestros propios juegos y proponerlos en los comentarios.

¿Qué significa esto?

Los experimentos LLR prueban el geocentrismo

Por si todavía los experimentos de M-M, Michelson-Gale, Sagnac, Trouton-Noble, Thorndyke-Kennedy etc. no probaron fehacientemente que la Tierra se encuentra en reposo absoluto, ahora resulta que un experimento realizado por los técnicos del proyecto Apollo, el Lunar Laser Ranging Experiment, lo ha hecho más-allá-de-toda-duda, y sin embargo parece que se ha silenciado.

Los experimentos LLR consisten en enviar múltiples pulsos láser desde la Tierra hacia un preciso punto de la superficie lunar donde ha sido colocado un retro-reflector que refleja cada pulso haz láser de vuelta hacia la Tierra. El objetivo inicial era medir la forma exacta de la trayectoria lunar promediando los datos de las distancias obtenidas en distintos tiempos.

Así está reflejado en la web de APOLLO:

. . . the time it takes for the pulse of light to travel to the moon and back [from the earth]. . . anywhere from 2.34 to 2.71 seconds, depending on how far away the moon is at the time (the earth-moon distance ranges from 351,000 km to 406,000 km). We can time the round trip to few-picosecond precision, or a few trillionths of a second.
http://www.physics.ucsd.edu/~tmurphy/apollo/basics.html

Retro-reflectores para el experimento LLR fueron ensamblados durante las misiones tripuladas Apollo 11, 14 y 15; otro fue también colocado por medio del vehículo espacial no-tripulado soviético Lunakhod 2. En total hay cuatro colocados en la Luna (hay 5 pero uno no funciona). Cada uno consiste en una serie de cubos (corner cubes) reflectores concentrados, que forman un tipo especial de espejo con la propiedad de reflejar un haz de luz entrante, y llegar a devolverlo en la misma dirección. Puede leerse más sobre reflectores lunares en la web oficial:
http://www.physics.ucsd.edu/~tmurphy/apollo/lrrr.html

Las pulsaciones del haz de láser se observan desde telescopios terrestres, y darían a los científicos la oportunidad de medir con precisión la distancia Tierra-Luna y así estudiar la forma de la órbita lunar. Se utiliza un haz láser porque esta luz puede enfocarse a grandísimas distancias con poca dispersión. Aún así, cuando llega a la superficie lunar el haz se ha dispersado hasta formar un círculo de unos 7 km de diámetro, y al retornar a la superficie terrestre alcanza hasta los 20 km de diámetro. Obviamente, la señal que llega a la Tierra es extremadamente débil, y para registrarla se necesitan largas exposiciones. Promediando la señal para un cierto tiempo, la distancia a la Luna podía medirse con una precisión de 3 cm; hay que tener en cuenta que la distancia media a la Luna es de unos 385.000 kilómetros.

De acuerdo al Heliocentrismo se tiene lo siguiente:
* Velocidad orbital de la Tierra alrededor del sol: 29,78 km/s
* Velocidad de rotación de la Tierra: 0,46 km/s (en el ecuador) – 0 km/s (en los polos).

A la hora de emitir el haz láser desde el telescopio terrestre, no tiene gran importancia la velocidad de rotación de la Tierra, puesto que para dirigir correctamente el rayo hacia el reflector sólo hay que tener en cuenta la velocidad relativa entre la superficie terrestre y la lunar. Sin embargo, esta velocidad rotacional debe ser tenida en cuenta para ubicar con precisión el telescopio receptor que captará la luz láser que retorna a la Tierra, pues si por ejemplo el receptor terrestre estuviera en el ecuador, éste debería estar situado entre 2,34x0,46 (1,07 km) y 2,71x0,46 (1,25 km) del punto en que se emitió el haz láser, dependiendo del lugar en que se encuentre la Luna (la luz tendrá entre 2,34 y 2,71 segundos de viaje). Si el experimento se realizase en el polo norte, no habría este inconveniente.

Pero la velocidad lineal tiene una desventaja superior, de acuerdo al heliocentrismo en esos 2,34-2,71 segundos la tierra se habrá desplazado una distancia entre 69,69 y 80,71 km en su trayectoria alrededor del sol. Por tanto, para el heliocentrismo el receptor debería colocarse, teniendo en cuenta la extensión de 20 km del haz laser, a una distancia entre 49,69 km y 60,71 km (a los que quizás habría que añadir los 1,07-1,25 km anteriores). Pero aún hay algo más, pues según los datos astrofísicos recientes el sol (con todo el conjunto de planetas) se está desplazando a una velocidad de 370 km/s hacia un punto de la constelación Leo. Por lo que habría que desplazar el receptor en unos 938 km más.
Prueba definitiva. La Tierra no se mueve, no rota.
Y ahora viene el punto primordial, los experimentos LLR comenzaron a hacerse desde 1969, y se siguieron haciendo durante bastantes años, lo que no está registrado en los libros es cuándo los científicos encargados de estos LLR observaron por primera vez –con un lógico asombro- que ¡el lugar receptor y el emisor coincidían!. Es decir, el mismo telescopio terrestre que lanza hacia la luna los pulsos laser los recibe sin ningún problema. No hay ningún desplazamiento.

Conclusiones:
- La Tierra está estacionaria relativa al sol (la velocidad de traslación es v=0), por tanto es el sol el que orbita alrededor de la Tierra.
- La Tierra está estacionaria relativa a la luna, por tanto la luna orbita alrededor de la Tierra.
- La Tierra no rota en torno al eje norte-sur terrestre (la velocidad de rotación es nula), sino que las estrellas y todo el firmamento rotan en torno de ese eje.

Pues bien, visto todo lo anterior, ¿tú qué opinas? ¿Tiene sentido lo expuesto, es verdad o es una trampa? Puedes participar con tus comentarios, es fácil.